Artificial Intelligence, Real Stupidity

Artificial Intelligence (AI) is becoming increasingly popular among service providers. This includes banks and search engines, this on the basis that it provides the same or a better level of service at a lower cost. This is all very fine until the AI goes wrong.

I have seen two examples of AI failure in the last 24 hours. These include Twitter permanently suspending a user for saying that he had killed a fly, and one of my own shortened Google links being banned for allegedly pointing to a child abuse web site when it actually pointed to a government web site on protecting children (https://goo.gl/1Nfo7 and https://www.esafety.gov.au/education-resources/iparent/online-safeguards/parental-controls). While the impact on the users is annoying in both these cases, there is a significant risk that AI failure will have serious impact on other people, including the risk of death.

In both cases, the AI engines appear to have been working on the words alone. There was no attempt to do a semantic analysis on the text. Had such a semantic analysis been undertaken, neither of these cases would have happened. Semantic analysis tools are available. That the people who implemented to the two AI engines did not see fit to include any semantic analysis shows an obscene failure to discharge their duties.

Unless, and until, those organisations that use AI instead of real intelligence achieve a reduction in the error rates of their AI engines by at least four orders of magnitude, I call a pox of all their houses!

A Worrying Example of Innumeracy

Introduction

Scientists can reasonably be expected to understand the tools of their profession. In the case of cosmologists, this includes telescopes, gravity detectors, clocks and computers, among other things. While a good understanding of pure mathematics may be helpful, a thorough grasp of those parts of applied mathematics that are relevant to their discipline is essential. For cosmologists, this includes Einstein’s Theory of General Relativity.

This post has been prompted by a self-declared accidental physicist whose biography on Twitter states “Maths is now more a trap than a tool.”. That statement could be disastrous for anybody who is less than fully secure in their own numeracy.

For reasons of probity, I have suppressed the identity of the individual concerned. I refer to him as “W”.

A View of Mathematics

Mathematics is often divided into pure mathematics and applied mathematics, and this is done for very practical reasons.

Pure mathematics can be regarded as a set of axioms, a set of rules of inference, and a set of theorems that can be derived therefrom.

Applied mathematics can be regarded as the application of selected theorems so solve everyday problems, such as planning a journey or adding up the cost of all your purchases in a shop.

Citing My Sources

For the sake of transparency, I feel it important that I include this screenshot of the W’s biography:

Biography

A Very Revealing Conversation

The image below captures the entire conversation between W and myself.

Conversation

I have numbered the key points in that conversation, and I offer below my observations on those points.

1. It constrains reasoned argument

The “If” in the image appears to be a typographical error. The words “It constrains reasoned argument” immediately reveal a lack of understanding of the rules of inference that are used in pure mathematics.

2. Both [Pure and Applied Mathematics]

Pure mathematics simply does not apply to quantum theory. Quantum theory is a mathematical model used in physics – it is an example of applied mathematics.

3. If Maths Makes the World It Applies To …

This sets a debating position which he overturns in point 4.

4. Maths Cannot

The words “Maths cannot” voids the debating position that he set.

5. Left and Right? Mathematically the Same

This shows a lack of understanding of the concept of ordering in pure mathematics, which is itself built on the concept of one type of relationship between two members of a set. I then used the concept of spaces and basis vectors to frame my next question to him.

6. Space is Einstein’s Space Time

This shows a lack of understanding of spaces and basis vectors, and a conflation of such spaces with space in cosmology. To assert that space is Einstein’s space time shows a lack of understanding of Einstein’s Theory of General Relativity.

7. You Asked What My Basis for Space Was

This conflates pure and applied mathematics.

8. All Space is in Space Time

We appear to have an epistemological issue here.

Conclusion

While the assertion that maths is now more of a trap than a tool might hamper W’s own work, the social damage this might cause if passed on to other people cannot be ignored. Educators in particular might need to be aware that students might be exposed to this sort of thing.

Professional Development Anybody?

Introduction

The topic of professional development (PD) seems to be a vexed issue among educators. Who should have it? What PD is most relevant to the individual? Is PD even needed? If so, how and when should it be undertaken? Who should deliver that PD?

I offer the experience below not by way of answering any of these questions but in the hope that it may shed some light on the discussions surrounding them. I have suppressed the identity of the person that prompted this post, as well as avoiding their particular area of expertise, with a view to saving embarrassment. I refer to that individual as “Q”.

Background

Q and I have known each other for years, and we routinely exchange ideas via Twitter. He had been teaching “X” for two years when the events below unfolded, and he felt that he was in command of his subject when it started. It turned out that his knowledge was both partial and faulty, though he did not know that at the time.

The Events

What started as a direct message (DM) unleashed a tsunami of learning for Q. He was puzzled by one small thing, and he sent me a DM about it. There then followed a long exchange of direct messages, including links to educational resources. It rapidly became apparent that we needed a face-to-face session, and the date, time and location were agreed.

I then prepared a PD session using a workshop approach. This included a session plan, handouts, and generating appropriate questions to ask of Q. The first task of the session was to correct Q’s misunderstandings, followed by a gap analysis, and ending with some delivery of learning. Everything was customised to Q’s context. This established a basis for what was to follow.

The face-to-face PD lasted for two hours, and Q was exhausted at the end of it. The amount of preparation time and effort needed for that session was about the same as would be needed for any session of that duration regardless of the number of participants.

The remaining PD was via direct messages, this perhaps contrasting starkly to the factory model of delivering PD to a group of people in a room.

Q then shared some of his students’ work for my comment, and it also became apparent that he was getting a firm grasp of the fundamental concepts. We then went on to the topic of grades. The grade descriptors figured very strongly here. Where Q saw a B and and B+, I saw a B and an A. Working in the industry as I do, I immediately understood the grade descriptors in both the work context and the educational context. Q did not have that advantage. The PD had moved from the phase of understanding the content to the phase of understanding how student work should be graded.

The final step of the PD was to bring in industry considerations, something that was beyond the scope of the curriculum, but that would nevertheless help to inform Q of the type of feedback that he could be giving to his students.

Q shortly afterwards expressed great gratitude for what I had helped him to learn.

Final Comments

The above may point to some perhaps intractable problems. If Q had been asked if he needed PD before all these events happened his answer would almost certainly would have been “no”. Even if he had said “yes”, how would decision makers made the necessary PD available to him? Where would they find the funding, the training provider, and the political will? Regardless of the answers to those questions, I think it is worthwhile pointing out that Q sought out his own PD, and this has benefited both himself and all his existing and future students.

In the Age of Information, Ignorance is a Choice

Introduction

This post arises from an accumulation of observations of many people for whom an appropriate description would be “willfully ignorant”. I have in the past been described as being “fiercely analytical”. I make no apology for being that way, and it is by being that way that I write the first sentence in this piece.

Background

Teachers have a number of legal, moral and ethical obligations towards those whom they teach. This includes accuracy of the information given, and making plain differences between facts, opinions and falsehoods. Such obligations also extend to anybody who seeks to impart knowledge to others. Search engines have made fact checking very quick and fairly easy. Anybody who fails to avail themselves of this is making a conscious decision to remain uninformed.

“But It’s Only a Theory!”

Words in English can have multiple meanings. The word “set” covers no less than two pages of definitions in the 1973 edition of the Shorter Oxford English Dictionary. The phrase “Theory of General Relativity” appears to be widely recognised. I have yet to find anybody who thinks that Einstein’s work was just a guess, that being another common meaning of the word “theory”. It seems reasonable to expect that any informed individual would be aware of that distinction.

For anybody who is not fully familiar with the theory of evolution, it is a well-substantiated explanation for the diversity of life on our planet. It is accepted as a fact in the scientific community.

The time has come to introduce Mike Pence and Christina Wilkinson, vice-president elect of the United States of America at the time of writing and headteacher of St Andrew’s Church of England Primary in Oswaldtwistle Lancashire respectively. Christina is on record as saying “Evolution is not a fact. That’s why it’s called a theory!”. This caused such a storm that Christina deleted her Twitter account.

Mike Pence is on record as saying in 2002 “The truth is [evolution] always was a theory [not a fact]” (YouTube video at time stamp 2:26). As far as I can ascertain, Mike Pence still holds this position.

Both of these individuals appear to remain uninformed.

Looking Forward

This is not the place to try understand the reasons behind the choice to remain ignorant. It is a question perhaps best left to educational psychologists. The question that does remain is how can educators encourage future adults to take take advantage of the great quantity of information that is easily accessible. I suspect the answer starts with each child’s first day at school.

A Rate of Learning

Acknowledgments

The inspiration for this post comes from this tweet by Heather Julian (Twitter @mathrules13) and re-tweeted by Jill B (Twitter @jillgrafton):

Background

I will take it as a given the readers are familiar at least one set of skill/attainment level descriptors going from “can recognise” to “can exploit”, and agree that different people have different levels of recall for different things. I will also take it as a given that readers are familiar with Maslow’s hierarchy of needs.

This post does not refer to any publications, scholarly or otherwise. It is merely one person’s thoughts, and it is intended merely to provoke discussion.

The Teaching-Learning Equation

There are a number of phrases associated with the acquisition of skills and knowledge from a source outside the learner, each phrase having its own level of acceptability in different contexts. Examples include “teaching”, and “delivery of learning”. My own sense is that such phrases can obscure the dynamics of the teacher-pupil situation. Given the context implied by Heather’s tweet, I propose a scenario where the teacher:

has full command of the subject
is totally self-confident
has excellent communications skills
has good empathy
has a good grasp of the pupil’s current knowledge base in the subject

(I can hear some of you thinking back to your own school days and thinking “I wish!”.) Also, to do justice to Heather’s question, I think that we need to focus on what is going on in the pupil’s mind (and here I am forced to rely on my own memories of school, as augmented by how some of my own students have demonstrated learning).

A Model of Learning

My own model of learning is constructivism. In the context of numeracy, a grasp of whole numbers is necessary before the idea of fractions can have any meaning, for example, and the rest of this post is written accordingly.

I find the words “truly remember” and “meet our standards” to be thought-provoking, as it raises questions about what level of memory is being envisaged, and whose standards are being applied during assessment. Using the “quadratic formula” as an example, memory may range from recalling “I know that phrase means something” to being able to write it down upon the instant (as well knowing what it is used for), and its consequent relationship to skill/attainment level descriptors.

Extending the words “truly remember” and “meet our standards” to what the learning experience means for the pupil can also be revealing. Again from personal experience at high school, I was in one cohort where everybody was expected to learn lines of poetry and recite them in class. I learned what I needed to in the preceding 48 hours, recited, and promptly forgot them one hour later. In terms of the teacher’s expectation that we should all enjoy poetry, it was for me a disaster: his standards were irrelevant to me at a personal level.

At the opposite extreme, and at the same school and at about the same time, I had a number of experiences that I found to be highly relevant. I have room here to describe only one of them. The subject was mathematics. The class had been working though material for a few days, and I was not quite sure of how all the bits and pieces fitted together. Towards the end, the teacher spoke a single sentence and everything suddenly fell into place. That learning has stayed with me for over 40 years, this in stark contrast to the poetry experience.

Discussion

Teachers may have aspirations for their pupils. Sometimes those aspirations are selfish. At other times they are focused on the pupil. I have memories of both from my school days. It is for this reason that I posited the scenario above.

We are now into the complex area of the teacher’s motives, skills, knowledge and abilities and the interaction of these with the pupil’s motives, skills, knowledge and abilities. I argue that it is this complexity that rules out any simple answer or answers to Heather’s question, and that perhaps we should instead be asking ourselves “What can I do to help this pupil towards self-actualisation in as quick and as efficient way as possible?”.

Conclusion

It’s not an easy job!

A Philosophy of Instructional Design

Acknowledgment

The inspiration for this post comes from Temitope Ogunsakin and his comment on this post where he asks “What would you say is your Instructional Design philosophy?”. This post is by way of answering his question.

Objective

The objective of this philosophy is to make the learning experience as easy and enjoyable as possible for the learner. This has two outcomes. Firstly, it maximises the effective of the learning experience for the learner. It also fulfills part of the social contract between educator and learner, that of mutual respect.

This philosophy uses a number of guidelines as a way of meeting that objective. Discerning readers will notice that I have avoided using the word “rules”, as rules tend to be prescriptive and thereby interfere with reaching the objective.

Assumptions

This philosophy makes a number of assumptions about the learner. At the risk of perhaps stating the obvious, it may be worthwhile making those assumptions explicit, and it provides readers with an opportunity to challenge those assumptions.

All Learning is Built on Previous Knowledge

While the claim “All learning is built on previous knowledge” may seem bold, and it sidesteps the question of how babies start acquiring knowledge, I would argue that it is a useful starting point for discussing later learning. By way of example, the teaching of grammar relies on learners being able to recognise sentences, which in turn relies of the recognition of words. In a similar fashion, the ability to use money relies on (among other things) the ability to recognise and understand the meaning of digits.

Different Learners Learn at Different Speeds

It is perhaps a common mantra that different learners learn at different speeds, so it is worthwhile checking a few sources to see how widespread this view is. A quick search on Google found this from the Board of Studies Teaching & Educational Standards NSW, this from the Australian Curriculum, Assessment and Reporting Authority, and this from the New England Complex Systems Institute, all of which support this view.

Adults and Children Learn Differently

Adults bring a number of skills and personal attributes into the learning situation that can be harnessed to good effect. These include, but are not limited to, life experiences across a wide range of subjects, independent research skills, and a thorough grasp of what they want to achieve from their learning.

All Learning Requires the Sharing of an Idea

With the claim “All learning requires the sharing of an idea” I can see readers saying “But what about psycho-motor learning? And affective learning?”. While subjects such as pure mathematics and philosophy are entirely cognitive, and the claim is unlikely to be challenged in those arenas, I would also argue that “the idea comes first” in both other areas. In the case of psycho-motor skills, the idea is often shared by way of demonstration, and followed by learner practice Examples include how to use a hammer, how to drive a car, and how to use a paint brush. With affective learning, the idea is often first shared by asking a question: “How would you feel if …?”, followed by a discussion. Agreeing the ground rules with a new cohort is another example.

Tasks Analysis

I have designed and used task-analysed teaching material from nearly 20 years, and I have found it to be one of the most effective tools in my educational toolkit. I have found that the ideal length of a learning task is between five and 15 steps.

The Guidelines

Audience identification: Unless I have a very good idea about what the learners already know, and what it is that they wish to learn, I have nothing to work with: I have no foundations upon which to present new ideas, and I have no direction as to which ideas I should choose. By way of example, I delivered learning in Microsoft project a group of older people who were experienced project planners using manual techniques and who wanted to learn how to use Project instead.
Matching the learning material to the learners’ existing knowledge base: Using the same scenario as above, I learned that my audience were in the business of installing water distribution infrastructure, so examples, exercises and questions about pipe laying, construction of pumping houses and supply of electrical power were obvious choices.
Bite sized chunks of learning: My comment on the ideal size of task-analysed activities translates well into other learning activities when it comes to planning the amount of material to be shared between signposts. Even in an extended whole group discussion, the learners themselves can raise such signposts, and the learning goes on to new ideas.
Structure: I regard structure as crucial. This is a direct consequence of the idea that learners build their new understanding on the foundation of previous knowledge.
Humour: Humour can be used tool, though not all learners seem to recognise it at the time. One cohort only came to understand the significance of a Mr Thread as the CEO of the Brazil Nut and Bolt Company in their coursework once they had finished their exams. Other humour can be injected ad lib while speaking.
Personal relevance: Without personal relevance, the learning material is likely to be less effective. The mathematics of the motor car was so interesting to one youth-at-risk that it turned his life around and he became a productive member of society.
Relevant technologies: The idea of of using technology as a ploy to engage students strikes me as at best silly. Having said that, I will make heavy use of technology where it is relevant. With the Microsoft Project course, it was appropriate to make the following design decisions:
- All the learning materials, apart from Microsoft Project itself, were entirely web-based. There were no paper handouts.
- All learners had individual computers, each with a copy of Microsoft Project already loaded.
- All learners were invited to bring one of their current projects along with them using whatever technology suited them.
- All learners were expected to work with both Microsoft Project and the web-based learning materials open on their computer at the same time.
- All learners were expected to leave the course with a fully functional copy of one of their projects in Microsoft project.
For the record, the course was extremely successful.
Immediate feedback: Some subjects, such a computer programming, Excel and Microsoft Project, have immediate feedback as an inherent quality of the product being learned. Immediate feedback is now normally built into web pages where this is relevant. When I write such pages, I build in such feedback at the design stage.

A Final Comment

I would never present all of the above as a single serving to anybody who was learning about instructional design. Having said that, it would not surprise me if experienced instructional designers read it in less than a minute, and then wanted to add their own ideas to the material presented here.

Maths from a Picture

The inspiration for this post comes from Brian Marks (Twitter: @Yummymath, web site www.yummymath.com/) with this tweet:

It seemed to me fairly easy to use that picture as a basis for writing a number of maths related questions, so I produced this document in Google drive. It has 13 questions related directly to the picture, and another 23 questions which use that picture as a starting point. The questions are in no particular order, and cover a broad range of topics and levels. While that document is a response to the question posed, I would hesitate to give it to any but the most competent and confident student of maths at year 11 or 12 level. It also goes well outside the area of pure mathematics, and provides some support in the area of physics. Having said that, it may provide an idea or two to anybody who cares to read it.

I would be very interested to hear your comments.

But What Use Does Maths Have Anyway?

Acknowledgment

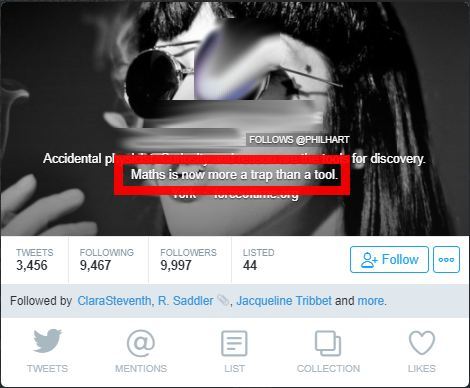
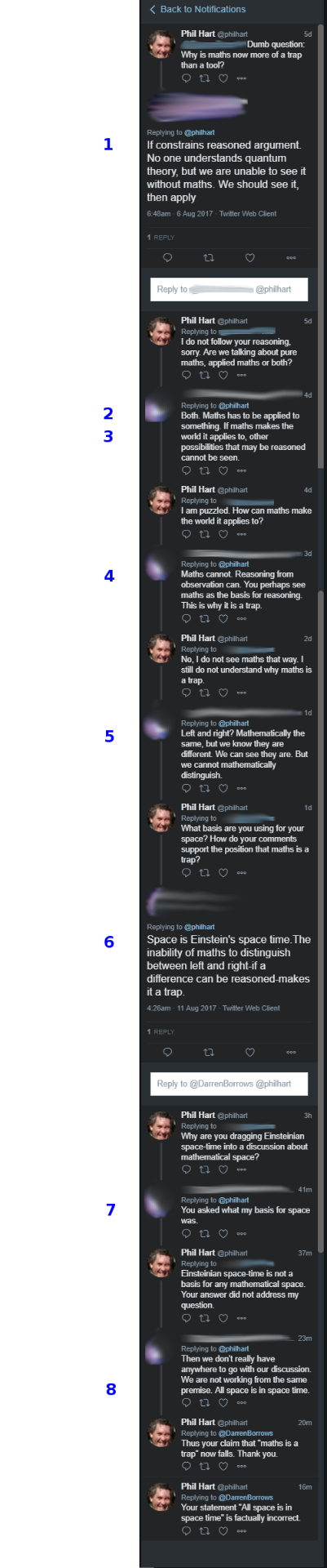
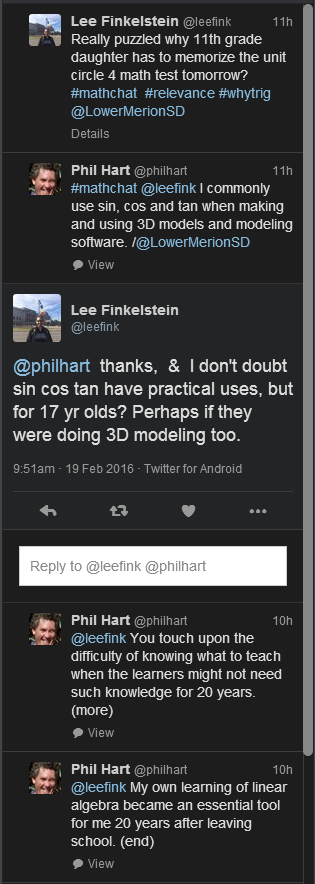
The inspiration for this post comes from Lee Finkelstein (Twitter: @leefink) with a tweet that resulted in the following exchange:

and it raises the question of why mathematics is taught in schools. The rest of this post shares my ideas on this question.

Assumptions Revisited

It seems to me that one of the purposes of schooling is to equip students with the knowledge, skills and attitudes to function effectively as adults once they leave school. It also seems to me that different students have different aptitudes and interests, and this has impact both on their performance at school and their learning. There is also the observation students will be “going into the world” where there will be jobs that do not exist at the time of their schooling.

Using Lee’s cri de coeur about why his 11th grade daughter needed to memorize things about the unit circle as a starting point, it is worthwhile commenting that every subject at school has relationships with other subjects, even though they tend to be taught in isolation from each other at high school. By way of example, mathematics is an essential component of the high school subjects chemistry, physics and engineering drawing. Mathematics is also an enabling tool for vast numbers of jobs in the workplace. Similar comments apply to the study of language its relationship with the workplace.

Speaking from personal experience, there were subjects that “bored me rigid” at school. It was not until well into my own adult life that I developed an interest in some of those subjects.

Discussion

The above raises the thorny and perennial question of what, and perhaps to a lesser extent when and how, educators (and by this I include non-teachers as well) should decide what should be learned. I have no answers to this question. All I can do in this context is to mention ideas and raise issues for other people to ponder and perhaps come up with their own answers.

It now seems appropriate to offer some personal experiences. When it comes to mathematics, its relevance to me was that I found it engaging for its own sake. There were three areas in particular (quadratic equations, linear algebra and statistics if you must know) that proved to be invaluable 20 years later, and saved my then employer in the region of US $10M/year. I found history and geography to be as dry as dust, and it was not until I explored the countries of western Europe as an adult that what little I had learned as a child served as an invaluable basis for learning about, and more to the point understanding, what it was that I was looking at.

Finally

I must now leave it for you, dear reader, to respond with your comments below. I look forward to hearing from you.

A Twitter Convention Observed

Introduction and Allegro

If you are familiar with my presence on Twitter (@philhart) you may have observed that I tweet on a range of subjects including Australian politics (#auspol), education (#edchat), mathematics (#mathchat) and security (#security), and I will sometimes tweet public replies with the intention of amusing the recipient. I have noticed that some people follow me for obvious reasons (they are educators, for example) and others for no reason that I can discern (but that is their privilege). Of particular note is people who add me to a special list on the basis of what seems to be a single tweet, with mathematics seeming to be the main cause for this. The risk that such people run is that they may be deluged by my tweets on other topics. To that end, I have abandoned convention and now commence my tweets with the relevant hashtags, leaving the content to follow, this with the hope that readers will know what I am tweeting about before having to read it all. I have noticed that some other people are doing the same thing. In light of this, I ask the following question:

Is it a practice that you agree with?

Is it a practice that you think should be promoted?

I look forward to reading your comments.

Maths Wars

Acknowledgment

The inspiration for this comes from Lina Zampichelli (Twitter: @micky_lina) with her post in the FS Teach Facebook group. (It is a closed group, so no link, sorry.) It links to an article in Canada’s National Post headlined “Math wars: Rote memorization plays crucial role in teaching students how to solve complex calculations, study says“.

I have been conscious of the recent shift towards “exploration learning” of mathematics, and I have felt uneasy about it, which unease I put down to a sense of nostalgia. Reading that article has made me re-appraise my unease, and the time has come for me to put my own viewpoint about how mathematics might be effectively taught so that it can be effectively learned.

I expect that I might upset a few of today’s younger teachers.

My Use of Mathematics as an Adult

Before describing my own experiences of learning mathematics, it might be useful for me state how I use mathematics in daily life. I do so as a matter of routine, and it is for on a par with reading, writing, speaking and listening: I could not function effectively without my skills in mathematics.

I use my estimation skills when shopping. I do so to check the reasonableness of the total payable. People “behind the counter” sometimes make mistakes, and I will discuss this when I think that I am being overcharged or undercharged. The estimation skill also applies when planning a major expense: what are approximate balances on the credit cards and bank account, what roughly is our monthly income, and what is the cost of the proposed expense. I can then make a yes/no/defer decision.

Basic counting along with addition and subtraction skills can be a time-saver, particularly in shops. At shops where I am known, rather than having to scan six or more items with the same bar code, or wait for the shop assistant to count them, I simply tell them the number, this saving time for both parties. When it comes to presenting cash, I often find that it is quicker and simpler to present money with the cents and low dollars value to the amount where I can receive a single bank note in return. Presenting $20.70 for a total of $10.70 means that I have less metal weighing down my wallet, and the giving of change is also quicker. (It also often brings a smile to the cashier, some of whom seem chronically short of change.)

When it comes to photography, the numbers associated with shutter speed, aperture and focal length always come into consideration when I compose a shot. Here we have gone away from simple counting, and moved into the areas of multiplication, division, and geometry.

Stepping up another gear, a grasp of statistics means that I am able to move from “average care” given by my local doctor, to “better care” with my doctor’s support. Whenever I consult him, I turn up with a printout of all the relevant data presented in statistical form, which allows him to make much better informed decisions. It also allows me to adjust my own medication very rapidly to respond to changes in my own body. A bout of influenza had a very strong impact on some of my vital signs, and ceasing one of my medications for the duration made my life a lot more survivable.

Raising the ante yet again, I use something called “vector matrix algebra” to solve problems with real-world impact. There is a bank of mains power outlets on the island bench in our kitchen. That bank looks a bit like a toblerone chocolate. The quickest and most effective way to find out which angles I needed to use to cut the pieces of wood was by using vectors. Anybody who writes software to display three-dimensional objects effectively on a computer screen needs a thorough understanding of vectors and matrices.

Pulling Out the Bones

In the examples above, as well as in other scenarios, I use the following skills as easily and as unconsciously as I read and write:

Counting
Addition and subtraction
Fractions in all their various forms: a/b, percentage, 12.3456
Multiplication, division
Geometry, both Euclidean and spherical
Trigonometry
Time, whether measured in femtoseconds or billions of years
Logarithms and exponentiation
Algebra and power series
Equations
Imaginary numbers
Base 2 (binary) and base 16 (hexadecimal) numerals
Statistical presentation and testing for statistical significance
Vectors matrix algebra
Calculus

At the bottom of all this lies my ability to count (1, 2, 3, …) which I was taught at a very young age. It was at about this time that I also noticed that not everything could be measured in whole inches, which lay the basis for my later grasp of fractions. I have a very clear memory of learning how to add double and triple digit numbers. Later came the rote learning of times tables, and I am very grateful for having been taught them. Procedures for long multiplication and long division soon followed, whence the concept of a remainder built on my observation of fractions of an inch. I was introduced to simple geometry at about the same time, this built on the concepts of space and measurement. At high school, these ideas were generalised into algebra, which itself served as a basis for learning calculus and the real-world applications thereof. Algebra was also used as the basis for learning vector matrix algebra, as was statistics.

What we have here is a structure of learning that was built on a foundation of a few simple concepts (counting, space, time, and observation) that my teachers helped me to assemble.

Putting this into a historical perspective, I have been the beneficiary of mathematicians whose efforts go back to the ancient Egyptians. The Arabs are credited with the idea of zero as a digit, but this is predated by its appearance in India in about the fifth century CE. Isaac Newton and Gottfried Leibniz are jointly credited with inventing calculus. More recently, vectors came about as the result of about a dozen people over 200 years. Let me put it another way:

If it had not been for the efforts of such people, I would still be counting by using pebbles on the floor of a cave.

Back to the Battlefront

The idea of “discovery-based learning” in mathematics strikes me as being fundamentally flawed. In my view, what is needed is a thorough discussion on what mathematical skills today’s children might want to use in their own adulthoods, and how best to equip them with those skills. Given the developmental benefits described in the article cited at the top of this post, I think it would be madness not to use rote learning to teach times tables.