Acknowledgment
The inspiration for this post comes from Lee Finkelstein (Twitter: @leefink) with a tweet that resulted in the following exchange:
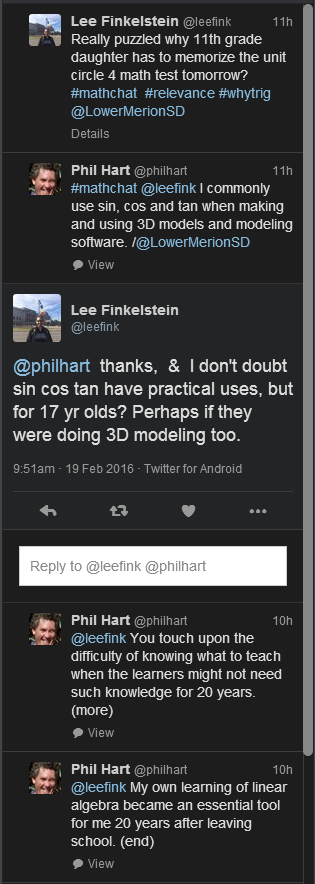
and it raises the question of why mathematics is taught in schools. The rest of this post shares my ideas on this question.
Assumptions Revisited
It seems to me that one of the purposes of schooling is to equip students with the knowledge, skills and attitudes to function effectively as adults once they leave school. It also seems to me that different students have different aptitudes and interests, and this has impact both on their performance at school and their learning. There is also the observation students will be “going into the world” where there will be jobs that do not exist at the time of their schooling.
Using Lee’s cri de coeur about why his 11th grade daughter needed to memorize things about the unit circle as a starting point, it is worthwhile commenting that every subject at school has relationships with other subjects, even though they tend to be taught in isolation from each other at high school. By way of example, mathematics is an essential component of the high school subjects chemistry, physics and engineering drawing. Mathematics is also an enabling tool for vast numbers of jobs in the workplace. Similar comments apply to the study of language its relationship with the workplace.
Speaking from personal experience, there were subjects that “bored me rigid” at school. It was not until well into my own adult life that I developed an interest in some of those subjects.
Discussion
The above raises the thorny and perennial question of what, and perhaps to a lesser extent when and how, educators (and by this I include non-teachers as well) should decide what should be learned. I have no answers to this question. All I can do in this context is to mention ideas and raise issues for other people to ponder and perhaps come up with their own answers.
It now seems appropriate to offer some personal experiences. When it comes to mathematics, its relevance to me was that I found it engaging for its own sake. There were three areas in particular (quadratic equations, linear algebra and statistics if you must know) that proved to be invaluable 20 years later, and saved my then employer in the region of US $10M/year. I found history and geography to be as dry as dust, and it was not until I explored the countries of western Europe as an adult that what little I had learned as a child served as an invaluable basis for learning about, and more to the point understanding, what it was that I was looking at.
Finally
I must now leave it for you, dear reader, to respond with your comments below. I look forward to hearing from you.
Hi Phil
Can I just clarify this – are you saying that you learned linear equations, sin, cos, etc in school, didn’t use it for 20 years, then were able to use it without relearning it?
Phil
Hello Phil C,
I used the basic trig functions as well as polynomials intermittently between school and that time, but I had not used linear algebra at all. My learning about linear algebra obviously stuck, and I have to thank my highly effective mathematics teacher for that. I had to look up the formulae for some of the statistical functions and significance tests (as well as learn about some new ones) at that time.
As a side comment, I still use these skills as a matter of course 40 years after acquiring them.
I hope this answers your question.
Phil H.
Hi
Thanks for answering.
So from that, I can presume that you have worked in a mathematical field – and in that case it makes perfect sense for you to have studied it in school.
The problem as I see it is occurs when everyone is asked to learn these kinds of unpractical, academic mathematics. All that achieves is building a dislike of school and the crushing of confidence.
The question as you say isn’t maths or not maths, but about choice.
Phil C
Hello Phil C,
You put it well when you say “[it’s] about choice”. It was my enthusiasm about maths at school that directed my career path into computers, and their use as a tool in industry.
I would guess that there is also the matter of perception by the student: if they don’t see a subject as being relevant to them in some way (i.e. choice) then they are much less motivated to engage with it.
Your comment about “unpractical, academic mathematics” has made me realize that there is a deeper question: “Unpractical for whom?”. For me, the question of whether of not a particular function is differentiable has direct impact on a whole class of computing problems, but for many people that question might be completely irrelevant.
Thanks for prodding my grey cell. 🙂
Phil H.